O cálculo do valor justo de ativos financeiros é uma etapa importante na contabilização de incentivos de longo prazo. Dentre as diversas alternativas que as empresas possuem para realizar a mensuração de opções de compra de ações, o modelo Black-Scholes é o mais adotado no Brasil.
Se você já possui familiaridade com as demandas contábeis de incentivos de longo prazo, continue a leitura para aprofundar ainda mais seus conhecimentos.
O que é o modelo Black-Scholes?
Black-Scholes é um modelo de precificação de opções desenvolvido por Fischer Black e Myron Scholes em 1973. O modelo revolucionou como as opções eram avaliadas e negociadas no mercado financeiro, e, atualmente, é o mais utilizado por empresas brasileiras para mensurar programas de ILP baseados em opções, como Stock Options.
Esse modelo é recomendado especialmente em casos de opções sem condições de performance associados ao valor, sem exercício antecipado e efeito do lockup; além de ser aderente para situações em que não haja negociações no mercado de opções com as mesmas características.
O Modelo Black-Scholes é baseado em certas premissas, como a volatilidade constante, o mercado eficiente e a ausência de restrições de venda das ações. Além disso, o modelo pressupõe que a opção será exercida somente no vencimento.
O modelo Black-Scholes não é recomendado para planos de opções com:
- Condições de performance associados ao valor
- Exercício antecipado
- Efeito do lockup
Componentes-chave do modelo Black-Scholes
O modelo Black-Scholes é fundamentado em cinco componentes que juntos fornecem uma estrutura para a precificação eficaz de opções.
Ele considera fatores como o preço atual da ação, o preço de exercício da opção, a volatilidade da opção, a taxa de juros livre de risco e o tempo até o vencimento da opção. Com base nessas variáveis, a fórmula calcula o valor teórico da opção, considerando a probabilidade de o ativo atingir determinado preço no futuro. Veja a fórmula matemática:
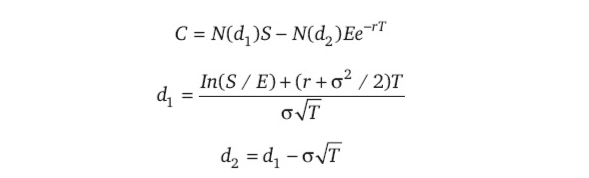
onde:
C = preço da opção de compra
S = preço da ação
E = preço de exercício
r = taxa de juros livre de risco
T = tempo até o vencimento da opção em anos
σ = desvio-padrão da taxa de retorno composto da ação anualizado
continuamente
e = base da função logarítmica, que é aproximadamente 2,7182
N(d) = probabilidade de que a variável aleatória de certa distribuição
normal seja menor que
Aplicação do modelo Black-Scholes em remuneração baseada em equity
Confira no exemplo abaixo uma aplicação prática do modelo. Perceba que apesar da aparente complexidade inicial, dadas as derivações matemáticas do cálculo, basta o valor de cinco variáveis para chegar ao preço da opção de compra.
Exemplo de cálculo do preço de opção de compra pelo método Black-Scholes
Preço atual da ação (S) = R$ 100
Preço de exercício (E) = R$ 90
Vencimento (T) = 1 ano
Volatilidade (σ) = 0,2 (20% ao ano)
Taxa livre de risco = 0,1 (10% ao ano)
Preço da opção de compra = R$ 19,99
Referência: Adaptado do Manual da Contabilidade Societária, 3ª edição.
Calculadora de Black-Scholes
A boa notícia é que não é necessário realizar esses cálculos à mão, graças à disponibilidade de diversas ferramentas digitais e planilhas projetadas para simplificar o uso do método.
Você pode fazer o cálculo sem dificuldade com a Calculadora de Black-Scholes do Basement. Para isso, é necessário considerar as seguintes informações:
- O valor da ação no momento em que a opção é outorgada;
- O valor estipulado para exercer a opção;
- O período restante até que a opção expire, medido em anos;
- A estimativa da flutuação esperada do preço da ação em um ano;
- A taxa de livre de risco do país de operação da empresa;
- A previsão dos ganhos em forma de dividendos (dividend yield), relevante apenas se o beneficiário não receber dividendos durante o período de carência;
Clique no banner abaixo e acesse gratuitamente a ferramenta:
Vantagens e limitações do modelo Black-Scholes
A principal vantagem de adotar o modelo Black-Scholes para precificar programas de ILP baseados em opções é a facilidade. Não é à toa que ele seja tão utilizado por empresas brasileiras. No entanto, dada a baixa complexidade, ele possui diversas limitações que devem ser consideradas.
Por exemplo, programa de stock option, com efeito lockup e/ou condições atreladas à performance, não devem usar o método Black- Schole, pois suas variáveis não consideram esses fatores.
Outra consideração importante é a incapacidade do modelo de incorporar fatores subjetivos e imprevisíveis que afetam o mercado, como mudanças no cenário político.
Mas apesar de suas simplificações e limitações, o Modelo Black-Scholes continua sendo uma ferramenta importante e amplamente utilizada na precificação de opções, tendo em vista que ele simplifica a oferta de incentivos de longo prazo no mercado.
Para além do modelo Black-Scholes, existem outros métodos relevantes para precificação do valor justo de opções. Entre eles:
- Modelo de Precificação de Opções Binomial: Outro modelo comumente utilizado para precificação de opções, que divide o tempo em etapas discretas e calcula o valor da opção em cada etapa, considerando a probabilidade de variações de preço.A complexidade desse método é considerada média, tendo em vista que não existe uma equação genérica e é possível adicionar regras específicas do plano de ILP no cálculo.
- Modelo de Precificação de Opções de Monte Carlo: Utiliza simulações estocásticas para estimar o valor de opções, considerando múltiplos cenários possíveis de evolução dos preços.Esse é um método considerado de alta complexidade, por contemplar um alto número de regras e variáveis e exigir uma modelagem para cada caso.
Vale salientar que a mensuração de valor justo é uma estimativa contábil que tem um grau de subjetividade e julgamento. Os modelos matemáticos são simplificações da realidade, sendo que o resultado da mensuração precisa fazer sentido para a companhia e demais pessoas, principalmente às lideranças de áreas financeiras.
E-book gratuito sobre contabilização de incentivos de longo prazo
O modelo Black-Sholes é apenas a ponta do icebeg que envolve a contabilização de incentivos de longo prazo. Para cada tipo de programa, existem métodos diferentes de mensuração dos ativos. Além disso, essa é uma das etapas do processo que qualquer empresa que tenha um plano de ILP precisa passar para contabilizar corretamente.
Preparamos um material que ajuda a entender as particularidades do processo de contabilizar stock options, ações restritas e outros tipos de planos no Brasil. Você aprenderá tópicos como:
- Valor Justo (Fair Value): Saiba como e quando mensurar o valor justo dos ativos financeiro.
- Modelo Black-Scholes: Entenda a lógica do cálculo do método mais utilizado pelas empresas para calcular o valor justo das opções de compra de ações.
- Avaliação 409A (Valuation 409A): Descubra as nuances do processo de avaliação do valor de mercado da companhia.
- Contabilização na prática: confira um caso real de correção no processo de contabilizar stock options;
Além disso, explicamos como você pode usar o sistema do Basement para descomplicar a contabilização de incentivos de longo prazo. Com a plataforma é possível gerar relatórios contábeis e tributários automatizados, configurar parâmetros específicos para cada plano, entre outras funcionalidades. Clique no link abaixo e acesse gratuitamente o e-book: